Lorentzian Classification: What It Is ? How it works ? + 10 Backtests Examples

In recent years, advances in machine learning and data analysis have led researchers to explore increasingly sophisticated mathematical frameworks. One particularly fascinating area of exploration is the use of Lorentzian geometry, a field deeply rooted in the mathematics of spacetime, to improve classification tasks. This approach, often referred to as Lorentzian classification, harnesses the geometry of hyperbolic spaces and Minkowski-style inner products (Lorentzian metrics) to represent data in a manner that can lead to improved performance for certain complex classification problems.

This article aims to explain what Lorentzian classification is, the key mathematical ideas that underlie it, and how it works in practice. Along the way, we will highlight its connections to hyperbolic embeddings, how it differs from traditional Euclidean methods, and what kinds of problems it is well suited to tackle.

Lorentzian classification refers to a strategy for performing classification tasks within a geometric framework inspired by Lorentzian geometry—an area of mathematics and physics that studies spaces equipped with a metric of mixed signature. Unlike Euclidean spaces, which have a positive-definite metric (all squared distances are positive), Lorentzian spaces feature a metric with one negative dimension and the rest positive. Such spaces are sometimes referred to as Minkowski spaces, and they form the mathematical backbone of Einstein’s theory of relativity.

Though Lorentzian geometry is traditionally associated with physics, it has begun to find applications in machine learning and data science. The idea is that when representing data, especially data with hierarchical or tree-like structures, embedding points into a Lorentzian (or hyperbolic) space can better capture relationships that are not easily represented in standard Euclidean space. In short, Lorentzian classification attempts to leverage the unique geometric properties of these spaces to improve the accuracy, interpretability, and efficiency of classification models.

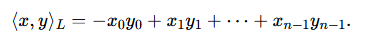
This metric, often referred to as Lorentzian or Minkowski metric, differs from the Euclidean one, where the inner product is always positive. The presence of a “negative” direction changes the geometry dramatically: it allows for certain curves, geodesics, and hierarchical embeddings that better reflect certain kinds of data structures.

2. Hyperbolic Geometry and the Lorentz Model:

Lorentzian classification is closely connected to hyperbolic geometry, a non-Euclidean geometry with constant negative curvature. One common model of hyperbolic geometry, known as the Lorentz model (or the hyperboloid model), represents points on the forward sheet of a two-sheeted hyperboloid defined within Minkowski space. Concretely, the n-dimensional hyperbolic space HnHn can be represented as:

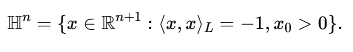
In this model, the distance between points is induced by the Lorentzian inner product. The geometry here naturally encodes hierarchical relations because distances grow exponentially with hierarchy depth—a perfect fit for data with tree-like structures, linguistic taxonomies, or complex hierarchical relationships such as those found in social networks or biological ontologies.

1. Better Representations of Hierarchical Data: Many real-world datasets contain hierarchical or graph-structured relationships. For example, consider a set of documents organized into categories and sub-categories, or a taxonomy of species branching down from a kingdom to specific species. Representing such data in a Euclidean space often leads to distortions: the data points become crowded in the center and relationships are not well captured. Hyperbolic spaces, and by extension Lorentzian models, naturally represent hierarchical structures with less distortion. Distances scale in such a way that the "leaves" of a hierarchy can be placed far apart while maintaining reasonable distances near the root, reflecting the underlying structure better than a flat Euclidean space.

2. Mathematical Convenience and Hyperbolic Embeddings:

Hyperbolic embeddings, using the Lorentz model, enable closed-form formulas for geodesics, midpoints, and other geometric operations that are more complex in alternative hyperbolic models. This simplicity makes training machine learning models in these spaces more tractable. When classifying data, the existence of a well-defined notion of “distance” and “angle” compatible with hierarchy can improve the separability of classes.

3. Improved Generalization and Separation of Classes:

Because Lorentzian geometry can spread out data more effectively at the periphery of the space, classes that are naturally separable along hierarchical lines may become easier to distinguish. For certain tasks—like classifying documents into increasingly fine-grained topics or separating biological taxa—embedding data into a hyperbolic or Lorentzian model can improve generalization. Models may achieve higher accuracy, particularly on complex classification tasks where flat geometries struggle.

The first step is to learn an embedding of the input data into a Lorentzian (or hyperbolic) space. If we consider a dataset {xi,yi}{xi​,yi​}, where xixi​ are feature vectors and yi∈{1,…,K}yi​∈{1,…,K} are class labels, we want to map each xixi​ to a point zizi​ in HnHn. This mapping can be done via a trained neural network or parameterized functions that place the data points on the hyperboloid. Techniques such as hyperbolic neural networks or Riemannian optimization methods are commonly employed for this step.

Unlike embedding in a Euclidean space, optimization in Lorentzian spaces requires careful handling of the geometry. For instance, one must ensure that updates to parameters keep points on the hyperboloid and respect the non-Euclidean geometry. This typically involves algorithms from differential geometry and Riemannian optimization, such as Riemannian gradients and projections onto the hyperboloid constraint.

Once data is embedded in Lorentzian/hyperbolic space, a classifier must separate different classes. In Euclidean spaces, linear classifiers like logistic regression or SVMs find a linear boundary. In a Lorentzian space, decision boundaries can be defined using geodesics (the “straight lines” of hyperbolic geometry) or hyperplanes determined by the Lorentzian inner product. A “hyperbolic hyperplane” might be defined by a point ww on the hyperboloid and the set of points zz that satisfy a particular geometric condition, such as a fixed Lorentzian inner product with w.

In practice, the classifier could take the form of a hyperbolic logistic regression or a hyperbolic neural network layer that learns weights and biases adapted to the Lorentzian geometry. The model’s parameters determine a decision rule that assigns class labels by comparing the embedded data point’s location relative to these learned hyperbolic separators.

Training a Lorentzian classifier involves selecting a suitable loss function and applying gradient-based optimization methods that respect the geometry of the space. A common choice is a softmax-based cross-entropy loss, similar to Euclidean classification, but computed in the hyperbolic space. Gradients must be computed using Riemannian gradients, ensuring that updates respect the geometry and keep embeddings on the hyperbolic manifold.

Several toolkits and libraries for hyperbolic embeddings are available, which handle the complexities of working on these manifolds. By using Riemannian optimization techniques, practitioners ensure that the parameters evolve correctly on the manifold, allowing the classifier to converge to a geometry-aware decision boundary.

1. Choosing the Dimension and Curvature:

Hyperbolic spaces are parameterized not only by their dimension nn but also by their curvature. Negative curvature is a key feature of hyperbolic geometry. Adjusting the curvature parameter can control how “tightly” the space bends, which in turn affects the embedding quality. Selecting an appropriate dimension and curvature can impact classification performance. Practitioners often tune these hyperparameters using validation sets, just as one would do with learning rates or network architectures in standard Euclidean training.

2. Initialization and Convergence:

Because working in a non-Euclidean space is more complex, proper initialization is critical. Points must start in regions of the hyperboloid that allow the optimizer to find meaningful embeddings. Moreover, care must be taken to ensure stable training. Modern optimization techniques, such as Riemannian Adam or Riemannian SGD, can help maintain numerical stability and achieve convergence to a good classification model.

3. Computational Complexity:

While Lorentzian classification can be powerful, it may come with increased computational costs compared to standard Euclidean methods due to the complexity of computing geodesics, exponential maps, and logarithmic maps on hyperbolic manifolds. However, efficient implementations and approximations are continually being developed, and the computational overhead often pays off with better representational capabilities and improved accuracy on complex tasks.

1. Euclidean vs. Lorentzian:

In Euclidean spaces, distances and inner products are simple. However, representing hierarchical data is challenging as Euclidean geometry tends to place data points in a relatively uniform space. By contrast, Lorentzian geometry naturally accommodates hierarchical relationships, allowing classes organized in tree-like structures or scale-free networks to be separated more efficiently.

2. Spherical and Other Non-Euclidean Geometries:

Other non-Euclidean geometries, such as spherical geometry, also offer benefits in certain contexts. For example, spherical embeddings can be useful for capturing cyclic or periodic data. But for representing hierarchies that branch out exponentially, hyperbolic (Lorentzian) geometry has proven especially powerful. It naturally encodes the exponential expansion of nodes in a tree, aligning well with how hierarchical data grows.

3. Connection to Hyperbolic Neural Networks and Word Embeddings:

Lorentzian classification does not stand alone; it is part of a broader trend in using hyperbolic geometry for machine learning. Hyperbolic neural networks, hyperbolic word embeddings, and hyperbolic graph embeddings all share the idea that certain data structures are more efficiently embedded in curved spaces. Lorentzian classification complements these developments by focusing on the classification step once the hyperbolic embedding is established.

1. Text Classification in Hierarchical Taxonomies:

Many text classification tasks require classifying documents into broad categories and then into more specific subcategories. Traditional Euclidean embeddings may struggle to represent such hierarchical constraints. Lorentzian or hyperbolic embeddings, followed by Lorentzian classification, can yield better semantic separations and improved accuracy. This has applications in organizing large corpora, news articles, or patent databases.

2. Bioinformatics and Taxonomic Classification:

Biological classification is inherently hierarchical. From kingdoms down to genera and species, life’s classification forms a tree. Embedding genetic sequences, protein structures, or species traits into hyperbolic space can highlight the tree-like structure of evolutionary lineages, making Lorentzian classification a natural fit for identifying classes of organisms or classifying sequences into related families.

3. Network Analysis and Community Detection:

Social networks, citation networks, and other large-scale graphs often have a hierarchical community structure. Lorentzian classification methods can be used to classify nodes into roles, community memberships, or functional categories by leveraging hyperbolic embeddings that capture the network’s structural properties better than Euclidean embeddings.

Research in this area is rapidly evolving. New theoretical insights continue to refine our understanding of how hyperbolic geometry interacts with machine learning models. As computational tools improve, training such models becomes more accessible to practitioners. Moreover, the method can be extended to more complex tasks beyond classification, such as regression, clustering, recommendation, and even generative modeling in hyperbolic spaces.

In the future, we may see Lorentzian classification integrated as a standard option in popular machine learning frameworks, making it as routine as choosing a non-linear activation function. We may also see specialized hardware accelerators or optimized algorithms that reduce the computational overhead of working with Lorentzian manifolds, thus making these techniques more broadly applicable.

Lorentzian classification represents a promising development at the intersection of geometry and machine learning. By leveraging the unique properties of Lorentzian and hyperbolic spaces, this approach provides a more natural representation for hierarchical and tree-structured data, enabling improved classification accuracy and interpretability. Though still a specialized technique, it aligns with the broader trend of exploring non-Euclidean geometries in machine learning to better reflect the complexity and structure of real-world data.

As the field matures, the concepts and methodologies of Lorentzian classification will likely become more streamlined, accessible, and widely adopted. For datasets that resist flattening into Euclidean space—and for tasks demanding a nuanced understanding of hierarchical relationships—Lorentzian classification can offer a powerful and elegant solution.